Beautiful algorithms used in a compiler and a stack based virtual machine ~Part 2. How the Pratt parser in the Monkey compiler works~
Photo by Joshua Ryder on Unsplash
This is the December 10th article for Wantedly 2021 Advent Calendar.
This is the second part of the series "Beautiful algorithms used in a compiler and a stack based virtual machine". In this series, I share algorithms, which I found interesting while implementing a compiler in Go by following two books, "Writing an interpreter in Go" and "Writing a compiler in Go" by Thorsten Ball. The specification of the Monkey language is explained in this page.
In this post, I will focus on the parser in the compiler. This is picked up in the second chapter in a book "Writing an interpreter in Go". I recommend you reading part 1 of this series, where steps taken by Monkey compiler to execute the souce code are descibed.
- Part 1. Design of the Monkey compiler
- Part 2. How the Pratt parser in the Monkey compiler works (this post)
- Part 3. How to compile global bindings
- Part 4. How to compile functions
- Part 5. What Monkey does not have, but Java has
For readers who would like to see my completed compiler, please take a look at my github repository kudojp/MonkeyCompiler-Golang2021.
This post consists of three sections. In the first section, I will make a general explanation on a parser in a compiler. Some different types of parsing algorithms are also introduced here. In the second section, a parser in the Monkey compiler is explained with two pairs of input tokens and the output tree. In the third and the final section is an explanation on Pratt parsing algorithms of the parser in the Monkey compiler. It will be explained in four steps with examples. Throughout this post, I put links to the codebase of my own Monkey compiler.
§1. Parser in a Compiler
In this section, I introduce the concept of a parser in a compiler and variations of parsing algorithms.
Role of a parser in a compiler
In a typical design of compilers, a parser takes tokens, which is the output of the lexer, and generates the tree structure named AST (abstract syntax tree). In statically typed languages, type checking is done in parsers.
Variation of parsing algorithms
Parsing of the tokens could be achieved in multiple algorithms including the top-down parsing and the bottom-up parsing.
The parser in Monkey uses the recursive descent parsing, which parses the tree recursively in the top-down manner. In particular, it is categorized into a Pratt parser, which is an improved recursive descent parser that associates semantics with tokens instead of grammar rules[1]. This was invented by Vaughan Pratt in his paper, "Top Down Operator Precedence" in 1973.
§2. Parser in the Monkey Compiler
In the previous section, I made a general explanation of a parser in the compiler. From this section, I will take a look at the parser in the Monkey compiler.
Like ordinary parsers which are described in part 1, the parser in Monkey takes a slice of tokens and generates the AST (abstract syntax tree). I will show two examples.
Please note that packages used in the input and output are mainly the tokens package and the ast package in the codebase. The parser package is not yet used in this section.
Example 1. Parsing of arithmetic operations and comparisons
The first example is the AST which is generated from arithmetic operations and comparisons.
// Input: slice of Tokens equivalent to
// (1 + 2) * 3 < 10 - (- 20)
[]Token{
{token.LPAREN, "("},
{token.INT, "1"},
{token.PLUS, "+"},
{token.INT, "2"},
{token.RPAREN, ")"},
{token.ASTERISK, "*"},
{token.INT, "3"},
{token.LT, "<"},
{token.INT, "10"},
{token.MINUS, "-"},
{token.LPAREN, "("},
{token.MINUS, "-"},
{token.INT, "20"},
{token.RPAREN, ")"},
}From the slice of Tokens above, the parser generates the AST below.
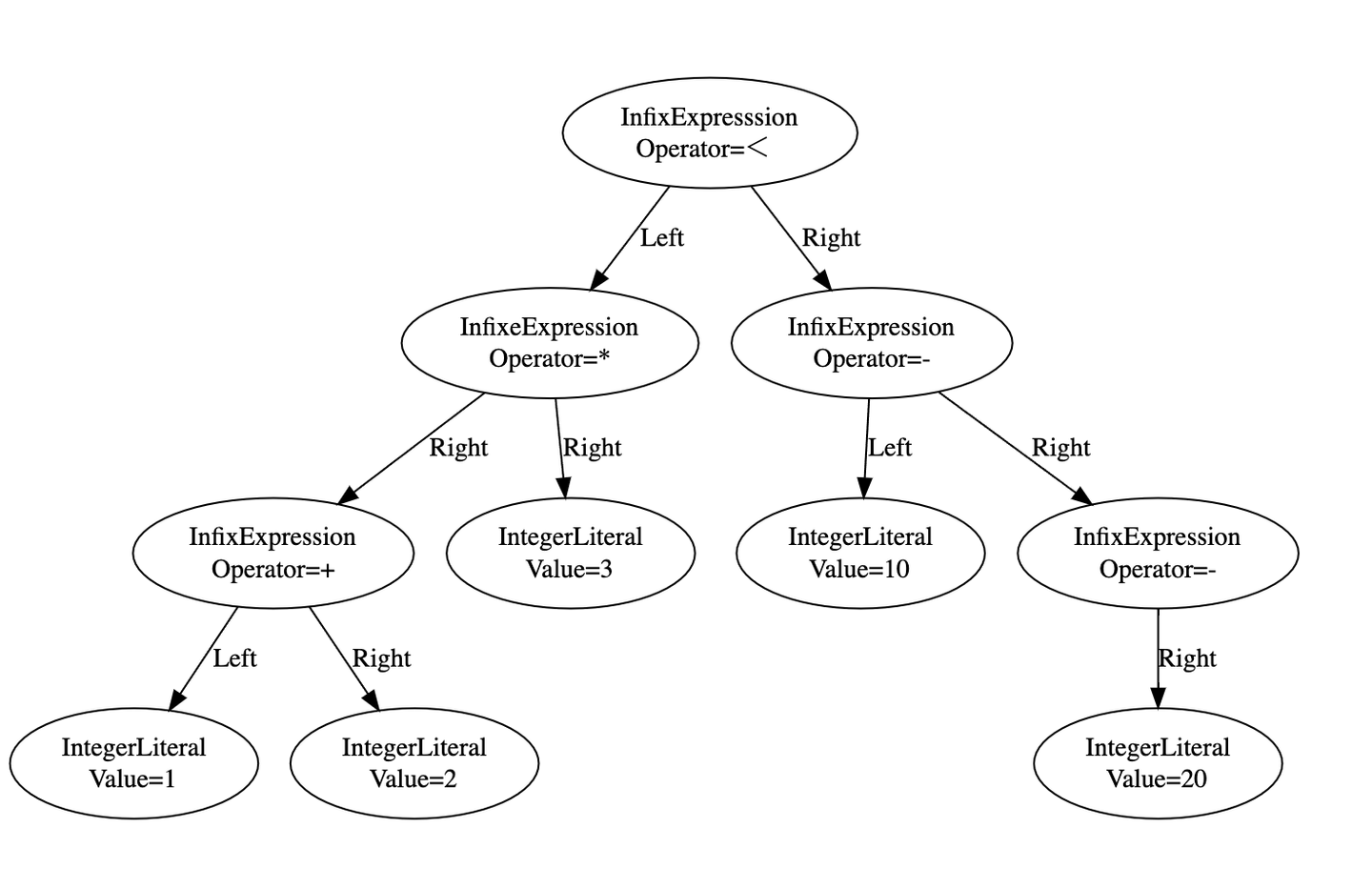
⬆️Drawn with Graphviz
In the graph above, the *first line in each node represents the struct type. The second line in the node and the edge labels represent the fields of the struct. All structs implements Node interface.
Two types of structs appear in the graph. Both of them, InfixExpression and IntegerLiteral, are introduced in the section 3 along with the parsing algorithm
Example 2. Parsing of a function literal
The second example is the AST which is generated from a function literal.
// Input: slice of Tokens equivalent to
// fn(x, y) {let a = x + y; return a; }
[]Token{
{token.FUNCTION, "fn"},
{token.LPAREN, "("},
{token.IDENT, "x"},
{token.COMMA, ","},
{token.IDENT, "y"},
{token.RPAREN, ")"},
{token.LBRACE, "{"},
{token.LET, "let"},
{token.IDENT, "a"},
{token.ASSIGN, "="},
{token.IDENT, "x"},
{token.PLUS, "+"},
{token.IDENT, "y"},
{token.SEMICOLON, ";"},
{token.RETURN, "return"},
{token.IDENT, "a"},
{token.SEMICOLON, ";"},
{token.RBRACE, "}"},
}From the slice of Tokens above, the parser generates an AST below.
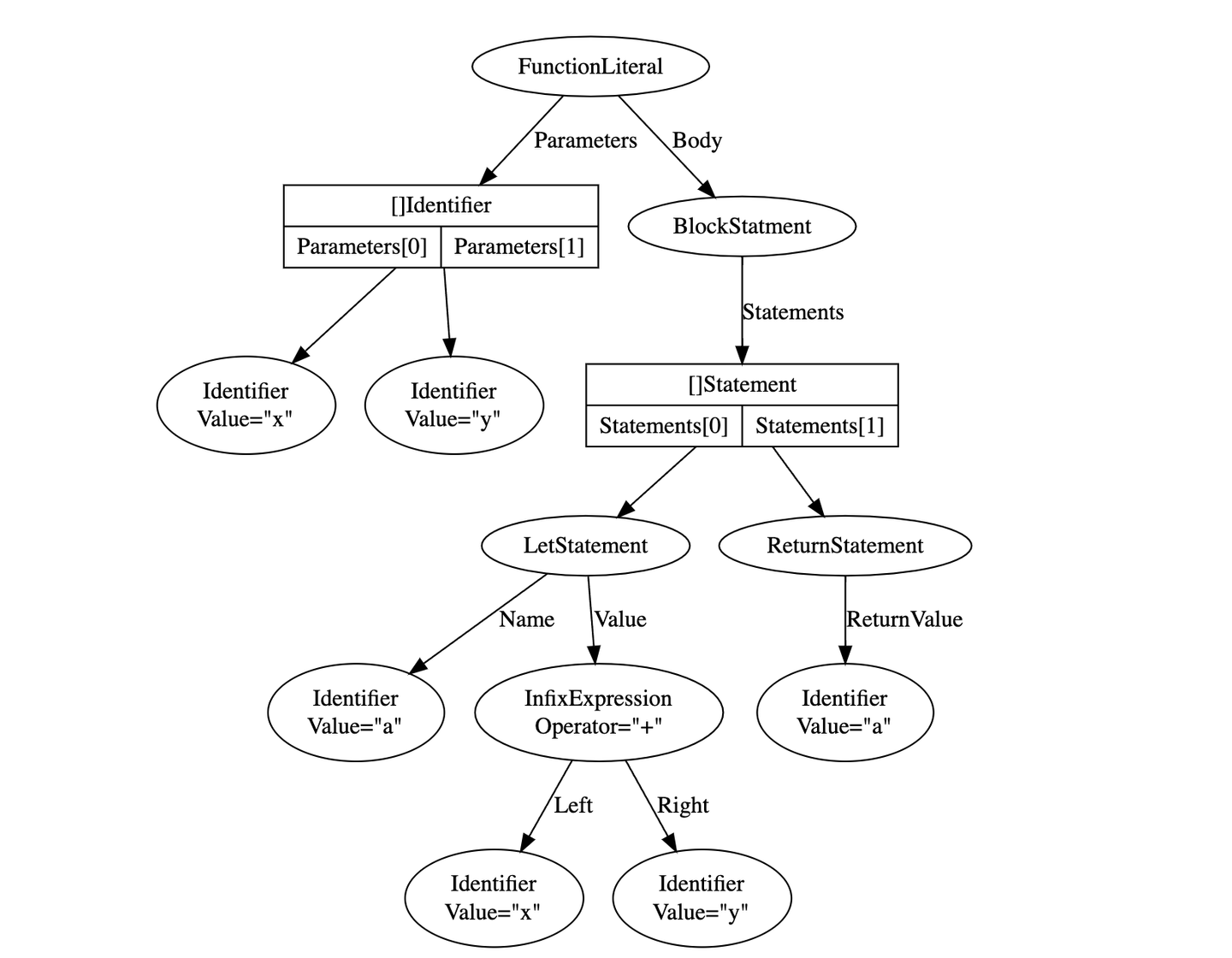
⬆️Drawn with GraphViz
The LetStatement node and the ReturnStatement node are generated from statements in the Monkey source code. The parsing algorithm of statements are not included in this post.
§3. Pratt Parsing Algorithm of the Monkey Compiler
In this section, I explain the core algorithm of the Pratt parser in the Monkey compiler in four steps. For simplicity, I narrow down the scope of the tokens to be parsed. Tokens parsed in this section are equivalent to an expression which is composed only of integer literals, arithmetic operators, parentheses, and comparison operators. That is, the goal in this section is to parse the expression like below.
(1 + 2) * 3 < 10 - 20Please note that the snippets in this section are not the same as the codebase in kudojp/MonkeyCompiler-Golang2021. Also, even though the parser parses the valid sequence of tokens correctly, it is not guaranteed to throw parsing errors as expected when an invalid sequence of tokens are given.
The compiler in Monkey uses a strategy to traverse a sequence of tokens in one path. The interface of the parser is below. Throughout this section, I implement parseExpression in this snippet.
type Parser struct {
curIndex int
tokens []token.Token
}
func (p *Parser) curToken(){
if curIndex < len(p.tokens){
return p.tokens[curIndex]
}
return nil
}
func (p *Parser) parseExpression() ast.Expression {
// TODO
}
func main() {
p := Parser{tokens: tokens}
p.parseExpression()
}Step 1. Enable to parse an integer literal
In this first step, I explain how to parse an expression which consists only of one integer literal.
// Input: a slice of Tokens equivalent to `1`
tokens := []token.Token{
{token.INT, "1"},
}The necessary change is only to parse a given token into the IntegerLiteral node and return it in the parseExpression method.
At the beginning of the parseExpression method, the parser looks for a function associated with the token type in the map named prefixParseFns and then calls it. If some token follows after that, the parser does the same thing with the map infixParseFns. That is, the parser looks for a function associated with the following token type in the map named infixParseFns and then calls it. The Latter one will be introduced in the next step.
I defined a new method named parseIntegerLiteral and register it in prefixParseFns. This is because the parser encounters an integerLiteral only at the beginning of the parseExpression method.
type Parser struct {
prefixParseFns map[token.TokenType]func() ast.Expression
curIndex int
tokens []token.Token
}
func (p *Parser) curToken(){
if curIndex < len(p.tokens){
return p.tokens[curIndex]
}
return nil
}
func (p *Parser) parseExpression() ast.Expression {
prefixFn := p.prefixParseFns[p.curToken().Type]
if prefix == nil {
panic(fmt.Sprintf("no prefix parse function for %s found", p.curToken().Type.Type))
}
parsedExp := prefixFn()
return parsedExp
}
// New
// This is registered in prefixParseFns
func (p *Parser) parseIntegerLiteral() ast.Expression {
lit := &ast.IntegerLiteral{Token: p.curToken()}
value, err := strconv.ParseInt(p.curToken.Literal, 0, 64)
if err != nil {
panic(fmt.Sprintf("could not parse %q as integer", p.curToken().Literal))
}
lit.Value = value
return lit
}
func main() {
p := Parser{
tokens: tokens,
// New
prefixParseFns: map[token.TokenType]func() ast.Expression{{
Token.INT: p.parseIntegerLiteral
}},
}
p.parseExpression()
}Step 2. Enable to parse an infix arithmetic operation
In this step, I explain how to parse an expression of an infix arithmetic operation like below. Expressions with multiple operators (e.g. 1 + 2 + 3) will be explained in the next section.
// Input: a slice of Tokens equivalent to `1 + 2`
tokens := []token.Token{
{token.INT, "1"},
{token.PLUS, "+"},
{token.INT, "2"},
}To parse this, the parser has to continue reading tokens which follows the first integer literal (1) in the parseExpression method. When encountering the plus operator, the parser looks for a function associated with the token.PLUS in the map prefixParseFns and then calls it, as described above.
That being said, I add the parseInfixExpression method and register it in the map prefixParseFns. This method is associated with infix binary operators (i.e. + - / *).
type Parser struct {
prefixParseFns map[token.TokenType]func() ast.Expression
curIndex int
tokens []token.Token
}
func (p *Parser) curToken(){
if curIndex < len(p.tokens){
return p.tokens[curIndex]
}
return nil
}
func (p *Parser) nextToken(){
if curIndex + 1 < len(p.tokens){
return p.tokens[curIndex+1]
}
return nil
}
func (p *Parser) parseExpression(precedence int) ast.Expression {
prefixFn := p.prefixParseFns[p.curToken.Type]
if prefix == nil {
panic(Sprintf("no prefix parse function for %s found", p.curToken().Type.Type))
}
parsedExp := prefixFn()
// when a token follows after the last one
for p.nextToken() != nil {
parsedExp = infix(leftExp)
p.curIndex += 1
}
return parsedExp
}
// This is registered in prefixParseFns
func (p *Parser) parseIntegerLiteral() ast.Expression {
lit := &ast.IntegerLiteral{Token: p.curToken()}
value, err := strconv.ParseInt(p.curToken.Literal, 0, 64)
if err != nil {
panic(Sprintf("Parse Error: could not parse %q as integer", p.curToken().Literal))
}
lit.Value = value
return lit
}
// New
// This is registered in infixParseFns
func (p *Parser) parseInfixExpression(left ast.Expression) ast.Expression {
parsedExp := &ast.InfixExpression{
Token: p.curToken,
Operator: p.curToken.Literal,
Left: left,
}
p.curIndex += 1
parsedExp.Right = p.parseExpression() // parse recursively
return parsedExp
}
func main() {
p := Parser{
tokens: tokens,
prefixParseFns: map[token.TokenType]func() ast.Expression{{
token.INT: p.parseIntegerLiteral,
}},
// New
infixParseFns: map[token.TokenType]func() ast.Expression{{
token.PLUS: p.parseInfixLiteral,
token.MINUS: p.parseInfixLiteral,
token.ASTERISK: p.parseInfixLiteral,
token.SLASH: p.parseInfixLiteral,
}},
}
p.parseExpression()
}Since a token exists after the first token, the parseInfixExpression method is called in the example. It returns the subtree whose root is InfixExpression node which corresponds to the infix operator. Its left subtree is the one given as an argument, which corresponds to 1, and its right subtree is the one which is generated by parsing the following token(s), which corresponds to 2, by calling the parseExpression method recursively.
The current parser cannot parse expressions with more than two infix operations correctly. This is because the precedence of operators have not been taken into consideration yet. The parser has to generate the resulting tree by considering it. For example, the asterisk operators are calculated earlier than the plus operators. The algorithm to enable this will be introduced in the following section.
Step 3. Enable to parse multiple binary operations
In this section, I will fix the parser to be able to parse an expression with more than two binary operators. I will show three examples first to make the image more clear.
// input example 1
// 1 + 2 * 3
tokens := []token.Token{
{token.INT, "1"},
{token.PLUS, "+"}, // lower precedenec
{token.INT, "2"},
{token.ASTERISK, "*"}, // higher precedence
{token.INT, "3"},
}// input example 2
// 1 * 2 + 3
tokens := []token.Token{
{token.INT, "1"},
{token.PLUS, "+"}, // lower precedenec
{token.INT, "2"},
{token.ASTERISK, "*"}, // higher precedence
{token.INT, "3"},
}// input example 3
// 1 + 2 + 3
tokens := []token.Token{
{token.INT, "1"},
{token.PLUS, "+"}, // same
{token.INT, "2"},
{token.ASTERISK, "+"}, // same
{token.INT, "3"},
}
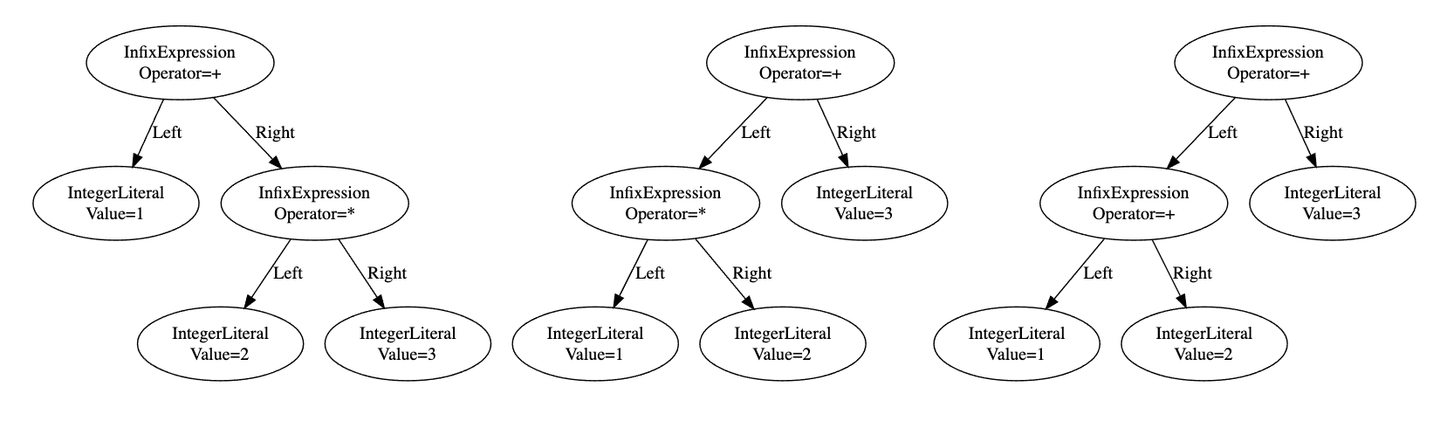
⬆️Written with Graphviz
The difference between the three examples are their operators. Since the precedence of asterisk operator is higher than that of plus operators, the parser has to generate a resulting trees so that their asterisk infix expression subtree should be nested in their plus expression subtree in example 1 and 2.
To make this possible, when the parser encounters a binary operator in the parseExpression method, it has to peek at the next operator. I explain with examples.
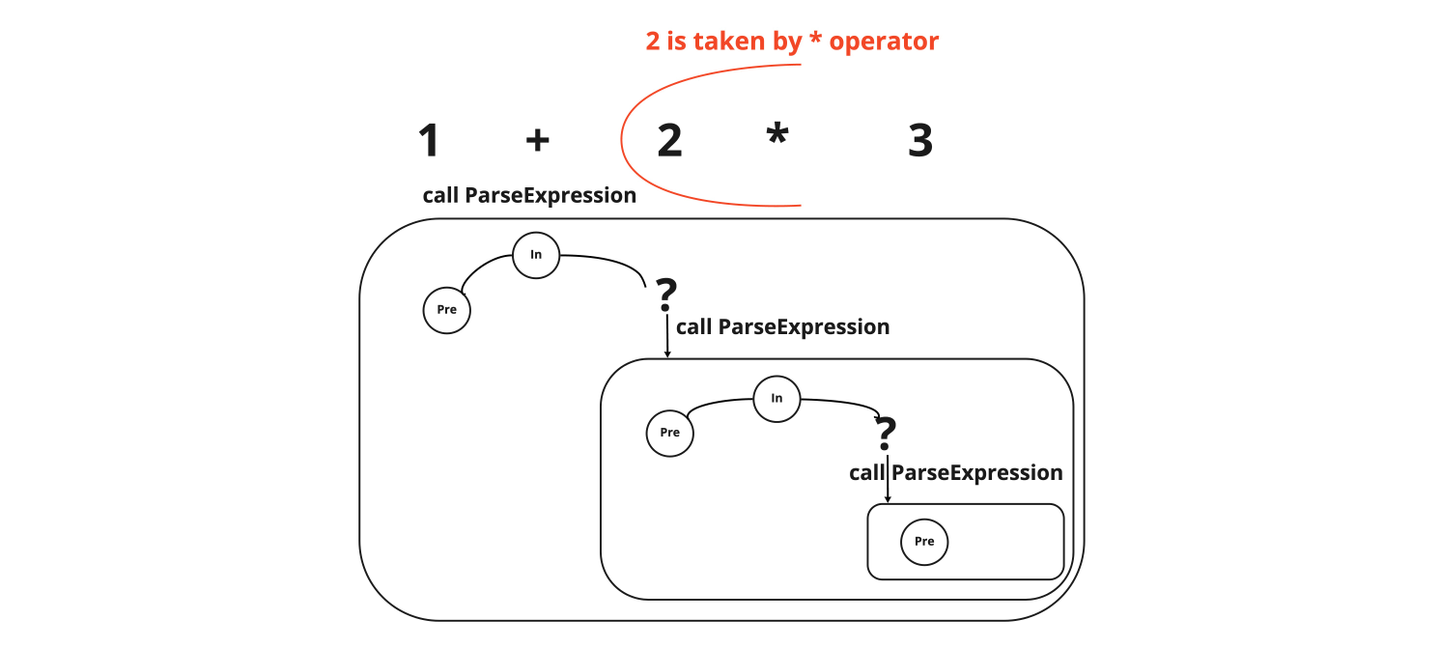
Example 1. To parse 1 + 2 * 3, when the parser finishes reading the plus operator in the parseExpression method, it peeks at the next operator. Since the next asterisk operator has higher precedence, the left subtree will be a node which represents only 1, and the right subtree will be that of 2 * 3. 2 is taken by the second operator. For this, the parser takes 1 as the end of the left expression and returns from the current call of the parseExpression method. In the caller, which is also parseExpression method, it takes + as the infix operator in that call.
Example 2. To parse 1 * 2 + 3, when the parser finishes reading the asterisk operator in the function parseExpression, it has to peek at the next operator. Since the plus operator has lower precedence, the left subtree will be a node which represents from 1 * 2, and the right subtree will be that of 3. 2 is taken by the first operator. For this, the parser takes the asterisk operator as the infix operator and calls the parseExpression method recursively to get the left subtree which begins from 2.
Example 3. To parse 1 + 2 + 3, either of the pattens above works. In the Monkey compiler, the parser handles this pattern the same way as the second one. (2 is taken by the second operator.)
I begin the implementation with these ideas. I define precedences of operators first.
var precedences = map[token.TokenType]int{
token.PLUS: SUM,
token.MINUS: SUM,
token.ASTERISK: PRODUCT,
token.SLASH: PRODUCT,
}
const (
_ int = iota
LOWEST
SUM // + -
PRODUCT // * /
)By using these precedences, I update the parseExpression method and the main method as below.
func (p *Parser) parseExpression(precedence int) ast.Expression {
prefix := p.prefixParseFns[p.curToken().Type]
if prefix == nil {
panic(Sprintf("no prefix parse function for %s found", p.curToken().Type))
}
parsedExp := prefix()
// New
// while a token follows after the last one and
// the precedence of the next operator is smaller than that of the last operator.
for p.nextToken() != nil && precedence < precedences[p.nextToken()] {
infix := p.infixParseFns[p.nextToken().Type]
if infix == nil {
return parsedExp
}
p.nextToken()
parsedExp = infix(parsedExp)
}
return parsedExp
}
func main() {
p := Parser{
tokens: tokens,
prefixParseFns: map[token.TokenType]func() ast.Expression{{
token.INT: p.parseIntegerLiteral,
}},
infixParseFns: map[token.TokenType]func() ast.Expression{{
token.PLUS: p.parseInfixLiteral,
token.MINUS: p.parseInfixLiteral,
token.ASTERISK: p.parseInfixLiteral,
token.SLASH: p.parseInfixLiteral,
}},
}
// Modified. LOWEST is given as an argument.
p.parseExpression(LOWEST)
}With these updates, the parser is able to parse expression with multiple operators correctly.
Step 4. Enable to parse parentheses
In this step, I enable the parser to parse an expression with parentheses.
1 * (2 + 3)In this example, the left child of the first asterisk operator should not be 2, but should be 1 * 2. This could be achieved easily by the parser calling the parseExpression method when it generates the left subtree of the node which corresponds to the asterisk operator.
In the current design, the parser could encounter a parenthesis only at the beginning of parseExpression function. Thus, a parenthesis could be considered as a prefix token.
I add a new method named parseGroupedExpression, which is associated with token.LPAREN, and register it in the map prefixParseFns.
After parsing the expression which is in the left parenthesis, the parser asserts that the right parenthesis follows. The updates in this step are below.
// New
// This is registered in prefixParseFns
func (p *Parser) parseGroupedExpression() ast.Expression {
p.curIndex += 1
// parse an expression which is in the parenthis
parsedExp := p.parseExpression(LOWEST)
p.curIndex += 1
if p.curToken != token.RPAREN {
panic(Sprintf("expected %s, but got %s", p.curToken().Literal, token.RPAREN))
}
return parsedExp
}
func main() {
p := Parser{
Tokens: tokens
prefixParseFns: map[token.TokenType]func() ast.Expression{{
Token.INT: p.parseIntegerLiteral,
// New
Token.LPAREN: p.parseGroupedExpression,
}},
infixParseFns: map[token.TokenType]func() ast.Expression{{
token.PLUS: p.parseInfixLiteral,
token.MINUS: p.parseInfixLiteral,
token.ASTERISK: p.parseInfixLiteral,
token.SLASH: p.parseInfixLiteral,
}},
}
p.parseExpression(LOWEST)
}Step 5. Parse comparison operators
In this final step, I enable the parser to parse an expression with comparisons.
1 < 2Comparison operators are parsed into the InfixExpression nodes the same way as binary operators. That being said, comparison operators should also be associated with the parseInfixLiteral method. All I have to do are two things. First, I definine the precedence of comparison operators. Then, I associate comparison operators with the parseInfixLiteral methood.
const (
_ int = iota
LOWEST
LESSGREATER // < >
SUM // +
// New
PRODUCT // *
)
var precedences = map[token.TokenType]int{
token.LT: LESSGREATER, // New
token.GT: LESSGREATER, // New
token.PLUS: SUM,
token.ASTERISK: PRODUCT,
}
func main() {
p := Parser{
Tokens: tokens
prefixParseFns: map[token.TokenType]func() ast.Expression{{
Token.INT: p.parseIntegerLiteral,
Token.LPAREN: p.parseGroupedExpression,
}},
infixParseFns: map[token.TokenType]func() ast.Expression{{
token.PLUS: p.parseInfixLiteral,
token.MINUS: p.parseInfixLiteral,
token.ASTERISK: p.parseInfixLiteral,
token.SLASH: p.parseInfixLiteral,
// New
token.LT: p.parseInfixLiteral,
token.GT: p.parseInfixLiteral,
}},
}
p.parseExpression(LOWEST)
}With these updates, the parser is able to parse comparisons.
I described the core algorithm of the Pratt parsing in five steps in this section. Feel free to examine the book and my github repository in more detail if you are interested in how other expressions and statements are parsed in the Monkey compiler.
§4. Summary
In this post, I first introduced the role and types of parsers in compilers in general. Then I show some illustrations of abstract syntax trees which are generated by the parser in the Monkey compiler to make your image more clear. Finally, I introduced the Pratt parsing algorithm in the Monkey compiler step by step.
References
[1] Wikipedia "Operator-precedence parser" https://en.wikipedia.org/wiki/Operator-precedence_parser#Pratt_parsing
